967. Minimum Falling Path Sum
Array Dynamic Programming Matrix
Problem - Minimum Falling Path Sum
Medium
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
Example 1:
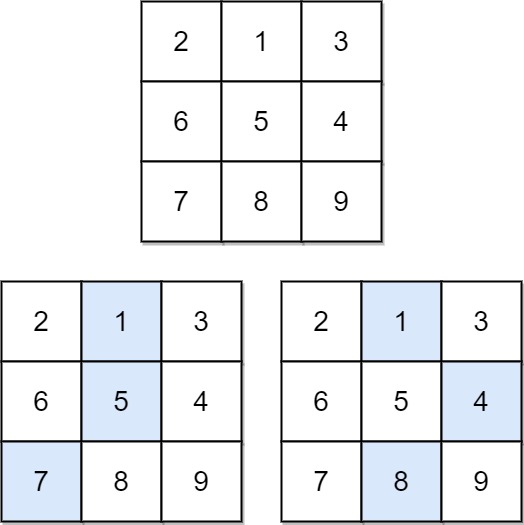
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]] Output: 13 Explanation: There are two falling paths with a minimum sum as shown.
Example 2:
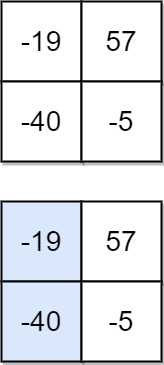
Input: matrix = [[-19,57],[-40,-5]] Output: -59 Explanation: The falling path with a minimum sum is shown.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 | |
Submission Stats:
- Runtime: 19 ms (71.29%)
- Memory: 18.4 MB (99.62%)