870. Magic Squares In Grid
Array Hash Table Math Matrix
Problem - Magic Squares In Grid
Medium
A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.
Given a row x col grid of integers, how many 3 x 3 magic square subgrids are there?
Note: while a magic square can only contain numbers from 1 to 9, grid may contain numbers up to 15.
Example 1:
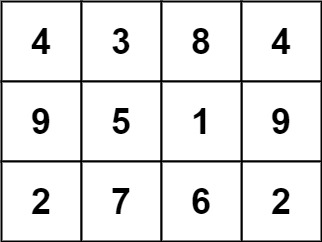
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]] Output: 1 Explanation: The following subgrid is a 3 x 3 magic square:while this one is not:
In total, there is only one magic square inside the given grid.
Example 2:
Input: grid = [[8]] Output: 0
Constraints:
row == grid.lengthcol == grid[i].length1 <= row, col <= 100 <= grid[i][j] <= 15
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | |
Submission Stats:
- Runtime: 0 ms (100.00%)
- Memory: 17.1 MB (100.00%)