79. Word Search
Array String Backtracking Depth-First Search Matrix
Problem - Word Search
Medium
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
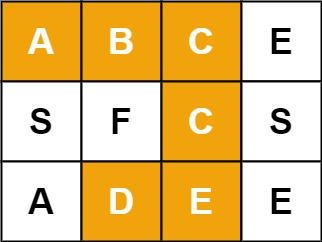
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" Output: true
Example 2:
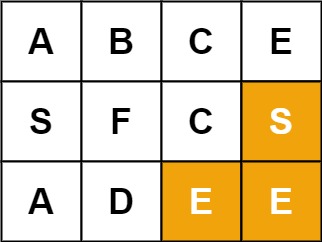
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE" Output: true
Example 3:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB" Output: false
Constraints:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15boardandwordconsists of only lowercase and uppercase English letters.
Follow up: Could you use search pruning to make your solution faster with a larger board?
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | |
Submission Stats:
- Runtime: 5104 ms (23.85%)
- Memory: 17.8 MB (87.82%)