51. N Queens
Array Backtracking
Problem - N Queens
Hard
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
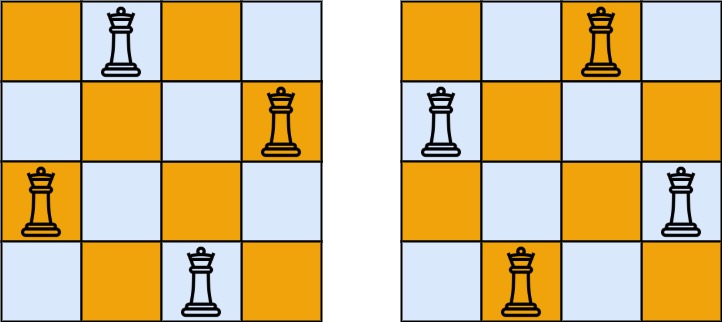
Example 1:
Input: n = 4 Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1 Output: [["Q"]]
Constraints:
1 <= n <= 9
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
Submission Stats:
- Runtime: 11 ms (72.51%)
- Memory: 18.3 MB (56.80%)