3733. Length Of Longest V Shaped Diagonal Segment
Array Dynamic Programming Memoization Matrix
Problem - Length Of Longest V Shaped Diagonal Segment
Hard
You are given a 2D integer matrix grid of size n x m, where each element is either 0, 1, or 2.
A V-shaped diagonal segment is defined as:
- The segment starts with
1. - The subsequent elements follow this infinite sequence:
2, 0, 2, 0, .... - The segment:
- Starts along a diagonal direction (top-left to bottom-right, bottom-right to top-left, top-right to bottom-left, or bottom-left to top-right).
- Continues the sequence in the same diagonal direction.
- Makes at most one clockwise 90-degree turn to another diagonal direction while maintaining the sequence.
Return the length of the longest V-shaped diagonal segment. If no valid segment exists, return 0.
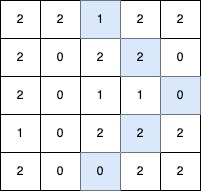
Example 1:
Input: grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]
Output: 5
Explanation:
The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,2) → (1,3) → (2,4), takes a 90-degree clockwise turn at (2,4), and continues as (3,3) → (4,2).
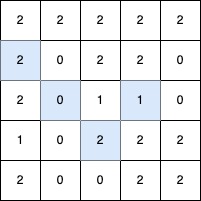
Example 2:
Input: grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]
Output: 4
Explanation:
The longest V-shaped diagonal segment has a length of 4 and follows these coordinates: (2,3) → (3,2), takes a 90-degree clockwise turn at (3,2), and continues as (2,1) → (1,0).
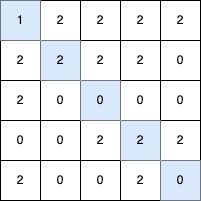
Example 3:
Input: grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]
Output: 5
Explanation:
The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,0) → (1,1) → (2,2) → (3,3) → (4,4).
Example 4:
Input: grid = [[1]]
Output: 1
Explanation:
The longest V-shaped diagonal segment has a length of 1 and follows these coordinates: (0,0).
Constraints:
n == grid.lengthm == grid[i].length1 <= n, m <= 500grid[i][j]is either0,1or2.
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | |
Submission Stats:
- Runtime: 4129 ms (38.18%)
- Memory: 525.5 MB (64.43%)