3459. Find The Minimum Area To Cover All Ones II
Array Matrix Enumeration
Problem - Find The Minimum Area To Cover All Ones II
Hard
You are given a 2D binary array grid. You need to find 3 non-overlapping rectangles having non-zero areas with horizontal and vertical sides such that all the 1's in grid lie inside these rectangles.
Return the minimum possible sum of the area of these rectangles.
Note that the rectangles are allowed to touch.
Example 1:
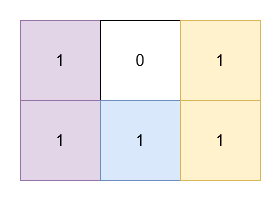
Input: grid = [[1,0,1],[1,1,1]]
Output: 5
Explanation:
- The 1's at
(0, 0)and(1, 0)are covered by a rectangle of area 2. - The 1's at
(0, 2)and(1, 2)are covered by a rectangle of area 2. - The 1 at
(1, 1)is covered by a rectangle of area 1.
Example 2:
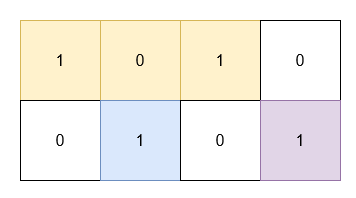
Input: grid = [[1,0,1,0],[0,1,0,1]]
Output: 5
Explanation:
- The 1's at
(0, 0)and(0, 2)are covered by a rectangle of area 3. - The 1 at
(1, 1)is covered by a rectangle of area 1. - The 1 at
(1, 3)is covered by a rectangle of area 1.
Constraints:
1 <= grid.length, grid[i].length <= 30grid[i][j]is either 0 or 1.- The input is generated such that there are at least three 1's in
grid.
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 | |
Submission Stats:
- Runtime: 6416 ms (19.04%)
- Memory: 17.9 MB (66.96%)