3335. Minimum Operations To Write The Letter Y On A Grid
Array Hash Table Matrix Counting
Problem - Minimum Operations To Write The Letter Y On A Grid
Medium
You are given a 0-indexed n x n grid where n is odd, and grid[r][c] is 0, 1, or 2.
We say that a cell belongs to the Letter Y if it belongs to one of the following:
- The diagonal starting at the top-left cell and ending at the center cell of the grid.
- The diagonal starting at the top-right cell and ending at the center cell of the grid.
- The vertical line starting at the center cell and ending at the bottom border of the grid.
The Letter Y is written on the grid if and only if:
- All values at cells belonging to the Y are equal.
- All values at cells not belonging to the Y are equal.
- The values at cells belonging to the Y are different from the values at cells not belonging to the Y.
Return the minimum number of operations needed to write the letter Y on the grid given that in one operation you can change the value at any cell to 0, 1, or 2.
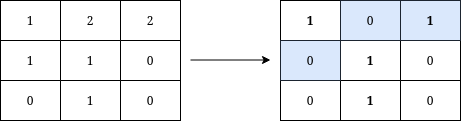
Example 1:
Input: grid = [[1,2,2],[1,1,0],[0,1,0]] Output: 3 Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 1 while those that do not belong to Y are equal to 0. It can be shown that 3 is the minimum number of operations needed to write Y on the grid.
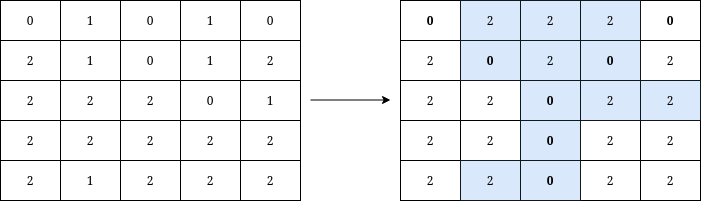
Example 2:
Input: grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]] Output: 12 Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 0 while those that do not belong to Y are equal to 2. It can be shown that 12 is the minimum number of operations needed to write Y on the grid.
Constraints:
3 <= n <= 49n == grid.length == grid[i].length0 <= grid[i][j] <= 2nis odd.
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | |
Submission Stats:
- Runtime: 67 ms (15.28%)
- Memory: 18.1 MB (24.41%)