2625. Increment Submatrices By One
Array Matrix Prefix Sum
Problem - Increment Submatrices By One
Medium
You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.
You are also given a 2D integer array query. For each query[i] = [row1i, col1i, row2i, col2i], you should do the following operation:
- Add
1to every element in the submatrix with the top left corner(row1i, col1i)and the bottom right corner(row2i, col2i). That is, add1tomat[x][y]for allrow1i <= x <= row2iandcol1i <= y <= col2i.
Return the matrix mat after performing every query.
Example 1:
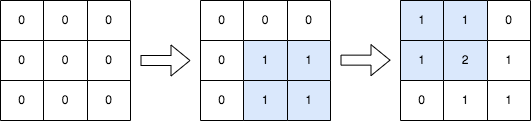
Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]] Output: [[1,1,0],[1,2,1],[0,1,1]] Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query. - In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2). - In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
Example 2:
Input: n = 2, queries = [[0,0,1,1]] Output: [[1,1],[1,1]] Explanation: The diagram above shows the initial matrix and the matrix after the first query. - In the first query we add 1 to every element in the matrix.
Constraints:
1 <= n <= 5001 <= queries.length <= 1040 <= row1i <= row2i < n0 <= col1i <= col2i < n
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
Submission Stats:
- Runtime: 245 ms (46.95%)
- Memory: 38.1 MB (63.85%)