2089. Maximum Matrix Sum
Array Greedy Matrix
Problem - Maximum Matrix Sum
Medium
You are given an n x n integer matrix. You can do the following operation any number of times:
- Choose any two adjacent elements of
matrixand multiply each of them by-1.
Two elements are considered adjacent if and only if they share a border.
Your goal is to maximize the summation of the matrix's elements. Return the maximum sum of the matrix's elements using the operation mentioned above.
Example 1:
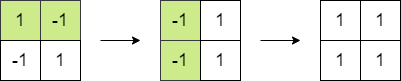
Input: matrix = [[1,-1],[-1,1]] Output: 4 Explanation: We can follow the following steps to reach sum equals 4: - Multiply the 2 elements in the first row by -1. - Multiply the 2 elements in the first column by -1.
Example 2:
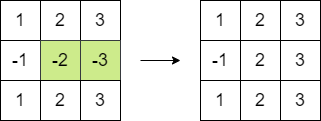
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]] Output: 16 Explanation: We can follow the following step to reach sum equals 16: - Multiply the 2 last elements in the second row by -1.
Constraints:
n == matrix.length == matrix[i].length2 <= n <= 250-105 <= matrix[i][j] <= 105
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | |
Submission Stats:
- Runtime: 84 ms (72.79%)
- Memory: 26.6 MB (15.19%)