1628. Count Submatrices With All Ones
Array Dynamic Programming Stack Matrix Monotonic Stack
Problem - Count Submatrices With All Ones
Medium
Given an m x n binary matrix mat, return the number of submatrices that have all ones.
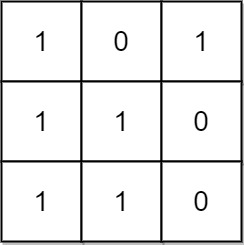
Example 1:
Input: mat = [[1,0,1],[1,1,0],[1,1,0]] Output: 13 Explanation: There are 6 rectangles of side 1x1. There are 2 rectangles of side 1x2. There are 3 rectangles of side 2x1. There is 1 rectangle of side 2x2. There is 1 rectangle of side 3x1. Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.
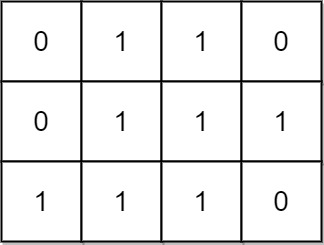
Example 2:
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] Output: 24 Explanation: There are 8 rectangles of side 1x1. There are 5 rectangles of side 1x2. There are 2 rectangles of side 1x3. There are 4 rectangles of side 2x1. There are 2 rectangles of side 2x2. There are 2 rectangles of side 3x1. There is 1 rectangle of side 3x2. Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.
Constraints:
1 <= m, n <= 150mat[i][j]is either0or1.
Solutions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | |
Submission Stats:
- Runtime: 774 ms (6.12%)
- Memory: 18.3 MB (99.87%)